Ampleforth is a token full of mystery. Its recent launch as a lending token on the AAVE v2 Market has led to many questions. My own recent pursuits have had me reading into options. I feel there is a lot of relevant ground to cover between the two, and I may be in a unique position to cover it, as I’ve previously written about Rebase (speculating on lending), its affects on Automated Market Makers, and the once great arb gap.
What’s special about Amples
Amples (AMPL) have a built in mechanism called supply smoothing. This is commonly known as Rebase, the name of function which initiates the process. This mechanism adjusts the supply every day to push the market price towards its peg. So 1 AMPL today could be 1.1 or 0.9 AMPL tomorrow, or really any amount. As all the intellectuals say these days, the amount of AMPL you have at any AMPL price is path dependent (non deterministic).
Very Basics
Lets say the price is $1.30 per AMPL and there is a supply of 1,000,000. Market cap of $1,300,000. (These numbers are made up and I’m trying to keep them at reasonable size).
Without other influences 300,000 AMPL would be issued and distributed proportionally to all holders. This would put 1,300,000 AMPL in existance and push the price to $1 per AMPL to maintain the market cap of $1,300,000. However this implementation of rebase has a “rebase lag” equal to 10, which reduces the impact by a factor of 10.
Accounting for lag, at rebase 30,000 AMPL will be issued and distributed proportionally to all holders. So any holder holding 100 AMPL now has 103 in their wallet. There would be 1,030,000 AMPL in existance, pushing the price per AMPL to $1.26 and change to maintain a market cap of $1,300,000
To a user this has an interesting affect. On one hand, they own the same percentage of the token’s total supply, on the other they hold a new number of units. Either helpful at estimating the approximate value at a glance, or terrible at navigating taxes, there are numerous intriguing side effects.
For one, Automated Market Makers (AMMs) often use a virtual balance, which needs to be updated when rebase occurs. For this reason most rebase tokens need to specifically integrate markets, giving the owner of the rebase contract unusual power over volume. Perhaps I’ll write more on that another time.
Uniswap V3 notably does not support rebasing tokens like AMPL. It will be interesting to see if evolution of other AMMs have similar restrictions. Of note, Sushiswap will be moving to virtual balances it at least some products.
Lending, but different
Lending AMPL starts typically. Deposit AMPL into the market contract. Eventually withdraw that amount of assets plus interest later. However, lending markets like AAVE don’t take into account rebase, so 1 AMPL loaned, means 1 AMPL to be repaid.
If rebase is positive, then the borrower keeps the extra issuance.
If rebase is negative, the borrower eats the loss.
Typically a borrower needs to do something with the borrowed asset to recognize these gains.
You’d think the lender is comfy knowing 1 AMPL is equal to 1 AMPL, but not quite. There is only so much debt versus collateral. A lender can approximate their hedge against rebase as proportional to the utilization rate minus any protocol fees. If 4 AMPL are borrowed for every 10, the lender definitely has 4, but the remaining 6 are exposed to rebase.
But its really so much more going on than that…
An Option If You Squint
Debt is measured in units, while amples themselves track balance as percent of the network under the hood. Borrowing and lending AMPL are effectively betting on the difference between these methods of measurement. The act of Rebase acts to settle these bets by issuing the new supply based on a volume weighted price feed. In effect, these are rolling bets where each days interest is a bet against that days rebase.
This simple distinction may just appear to be a bit of chaos magic, but it nuanced differences have an impact on market participation. I struggle to lay this out clearly as a summary, so fuck it we are gonna squint hard into way too much detail.
The Breakdown
The Token Dissection
The token is a store of value. Its a contract that manages tracking ownership. Ownership of a network has several factors
Issuance - The rate at which the supply in circulation is altered
Total Supply - The total units representing ownership of the Token
Balance - The amount of the total supply that a particular address holds.
Frags (unique to rebase) - The fraction or percent of the network that a particular address holds.
Most tokens don’t track Frags. Issuance is directed at a subset of the total holders and changes the percentage of the network every address holds.
With Ampleforth, issuance is directed proportionally across all holders and does not change the percentage of the network every address holds.
If the supply of a token never changed, than frags and balance would be effectively the same way to measure. However if the supply does change, and Balance is a function of Frags, than Frags is the true measure of Balance, and Balance is just anchoring Frags to a price feed. This may seem like a simple slight of hand, but it has big implications in lending.
Trading Nuance
Trading can be simplified as battle for balance between supply and demand on a market. Typically Token Issuance is abstracted from the market. This is because new supply is going to specific players, and most market participants are not affected. The supply and demand on the market remains the same unless the recipient of issuance brings that new supply to the market at an uncertain future time.
Early in its existence, Ampleforth team had expressed that the supply on market would not instantly react to rebase. Largely this was because bids would need to be adjusted to reflect the change in supply. Quite literally, it came as a surprise to everyone how things played out.
Automated Market Makers had a huge impact on AMPL markets since they set a price based on balance. Once AMMs are integrated into the rebase function for safety, they then have an instant recognition of the change in balance and reprice automatically. This created a pretty cool arbitrage gap between Centralized Exchange order books which went stale vs Uniswap where price instantly reacted.
Importantly, AMMs have large prevalence; Unlike other tokens where issuance does not have an immediate impact on market price, AMPL’s proportional supply change directly updates the balance of AMMs and therefore has instant impact on market rates. This is a formal event which occurs daily.
Lending Nuance
My brain hurts just trying to sort all this out, so bare with me.
Token - see above
The below track units based on Token Balance (not fracs)
Lending Supply - The supply of Token available to be lent
Lending Rate - The interest rate paid to Lenders on the units owed in the Token
Borrowed Amount - The supply of Token actively borrowed from Lending Supply
Borrow Rate - The interest rate paid by Borrowers on the units owed in the Token
Utilization Rate - Borrowed Amount / Lending Supply
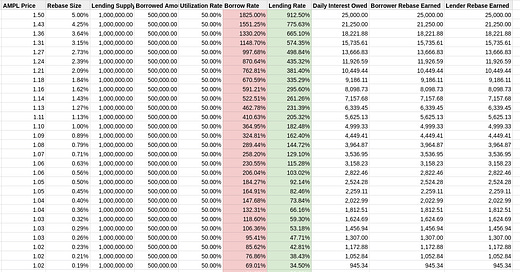
Lets begin with some charts, first for positive rebase.
Borrow Rate = (Rebase Earned / Borrowed Amount) * 365
This should allow us to see how much interest a borrower would have to pay to break even. Note that because the lending market depicted is only 50% utilized, the lender is still earning half the rebase.
In this set up at a price of $1.50 per AMPL, borrowers would have to be paying 1825% APR for 24 hours for lenders to break even even though the rebase size is only 5%.
This is because while the 500,000 AMPL are owed by the borrowers, they’d be holding 525,000 AMPL after rebase.
Then we have negative rebase
In this set up at a price of $0.50 per AMPL, borrowers would have to be earning 1825% interest on whatever they are doing with the borrowed funds just to break even. They’d collectively owe 500,000 AMPL while only holding 475,000.
In both we notice that the lenders are hedged from rebase. A portion of the rebase they would have felt in either direction is instead captured by the borrowers. However because the pool is not fully utilized they are still exposed to some rebase.
Quick Comparison
What if we lent ETH, and assume all borrowers trade for DAI? What’s that borrow rate for the same percent moves assuming profit is difference between USD value and ETH value?
Well would you look at that! If ETH is at 3000, and faces a 5% downward moved like our $1.50 AMPL, it too would need to be paying 1825% to make up for losses vs the short asset. However we don’t see that behavior reflected in the market paricipants…
Speculating the difference
While it appears the profit made from borrowing AMPL before a 5% rebase is the same as borrowing and selling ETH before a 5% drawdown, a key difference is that profit is locked in as held units with AMPL while ETH at close must be timed.
However in a competitive market delays will be punished with more interest. So the value may come from somewhere deeper.
With ETH you must ride out the 5% drawdown. With AMPL you can set your watch to the 15 minute window a 5% drawdown will occur.
Consider the AMM attack surface
As mentioned earlier, AMMs often use a virtual balance, which needs to be updated when rebase occurs. If the update does not occur in the same transaction as a rebase, the pool may be open to an attack.
The attack is structured as following.
Rebase occurs. The supply changes, and is reflected in each accounts balance on the token level. This difference is not reflected on the pools virtual balance
Attacker enters pool with very large size, perhaps funded through flashloan.
Attacker calls function (Sync/Gulp) to update pools local virtual balance, which then distributes rebase proportionally across all participants, giving the attacker a large share of other peoples rebase.
Attacker exits pools.
If 2, 3 and 4 are all in the same transaction an attacker can significantly capture a large sum of value without much price risk. To prevent this, the rebase contract is designed to call Sync/Gulp in the same transaction rebase occurs
Applying this attack to Lending
Rebase takes a price change and settles in units once daily. These units remain the same (outside of transfers, etc) until the next rebase. The rebase itself, reflects the 24 hour average price of AMPL.
The above chart was 1 day worth of interest. 1825% charged over 24 hours at 1.50. But what if a borrower is only borrowing for a few blocks before rebase and a few blocks after. Lets say 1 min.
Here we see to break even, a smart borrower would need to pay exorbitant rates if they only maintain debt for a minute and that minute surrounds the action of rebase. If they pay less, that’s profit recognized in a single minute. A riskless opportunity given AAVE interest maximum is being proposed around 10,000% vs the 2,628,000% profit here
Summarizing the problem
This lending model is not able to price risk accordingly for lenders, while giving borrowers an eye into the future. The entire battle gets pushed to a single block. Smart lenders will fight to exit pre rebase (on positive, similar to reverse but different on negative). Smart borrowers will fight to get in just before. We need to have a more structured field of entry and exit, else we have such a narrow window of free for all execution. We need to expect 100% utilization cases because of this jockeying where people can’t get out, because everyone else is pressured to push that limit to the max around the moment of rebase.
Consider Everlasting Options
Paper can be found here.
Here are three relevant quotes to catch you up on them if you don’t have time to read the full paper. Embellishments are my own.
First we see its designed with daily settlement in mind
If funding is paid once per day, this equivalent portfolio consists of one half an options contract expiring today, one quarter of an options contract expiring tomorrow, one eighth of an options contract expiring the day after that, and so on. All of these contracts have the same strike as the everlasting option itself.
Its design is informed by an exponentially-weighted moving average. Rebase is based on a volume weighted moving average. I don’t expect that will have much impact as we can curtail how we interpret rebase to our needs.
What I do know is lenders are seeking hedge from volatility so the protection against sudden drops seems to satisfy the desire sought with lending.
The framework can also be used to price a perpetual option whose strike is an exponentially-weighted moving average of the underlier price over time. This is because the expiring equivalent, the floating-strike Asian option, can also be priced, although doing so is not simple.
Owning such a put would effectively always allow an ETH holder to sell their holdings at, say, the exponentially-weighted average price of ETH with a half-life of one day, protecting her against sudden drops in the price of ETH.
Because the strike would automatically follow the price of ETH, it is possible that a single such product could fulfill the hedging requirements of the majority of ETH holders. This could potentially consolidate much of ETH options liquidity and volume into a single market.
This has a focus on the movements just before and after as important to its design. Which is exactly the kind of model we are looking for to address the attacks described above.
When reasoning about the behavior of a perpetual derivative around funding payment time, it is best to think about what happens either immediately before, or immediately after, funding is paid.
So we have Rebase, which is executed once per day and which is informed by a weighted moving average of price of AMPL over each day. If we replace ETH in the example, AMPL is already doing much of this work, but without a formal way of trading this exposure.
We have seen an attempt and trading exposure through lending, which seems inadequate. Perhaps following a model like this which seems very much aligned with mechanisms already in place with Ampleforth could be a better approach.
Why there’s a part 2.
Well I was gonna write this all at once but I went on vacation and I’m still trying to work out some of the entry and exit mechanics, but I realized I was letting people get actively rekted by not making more noise. So more to come on how to make options, and I’m not gonna edit it down cause I’m lazy.
This is a great thread of people working the ins and outs of SQUEETH that cover basically the issues I’m still tweaking on around how to balance drift most optimally.
I kinda already made it a gov post
And a follow up gov post
Teasers sheets of what could be possible everlasting options with AMPL, which due to rebase, could add no additional oracles (no more trust assumptions than AMPL itself. No extra price feeds)
Notice how the Difference column shifts on each side of the last rebase price marked with the yellow column and the dividing line.
First Positive
And now Negative.